[Day 10] Math for AI - Data visualization & Probability theory Ⅱ

📍 Data visualization - graphic tools

  🔥 matplotlib 

    - 대표적인 시각화 도구로 다양한 graph지원과 pandas 연동

    - pyplot 객체를 사용해 데이터 표시(flush 되기 떄문에 객체로 다루기 힘듬)

    - conda install matplotlib -> import matplotlib as plt

    - graph는 원래 figure 객체에 생성되고 figure안에 axes로 구성되는데 여러개의 axes를 생성할 수 있음

    - 단점: argument를 kwargs로 받고 또 고정된 argument없어 확인이 어려움.

 

    - color: float:흑백, RGB color, predefined color 사용

    - line style: dashed, dotted 등이 존재하고, 필요할 때 찾아쓰자!

    - title: plot위에 title을 만들어 줌(latex 타입의 표현도 가능 - 수식 표현 가능)

    - legend: 범례 표시함, loc위치 등 속성 지정

    - grid & xylim: graph 보조선을 긋는 grid와 xy축 범위 한계를 지정

 

  🔥 matplotlib graph

    - scatter(산점도): marker - scatter 모양 지정    /     s - 데이터의 크기를 지정(데이터의 크기 비교 가능)

    - bar chart: 설정으로 옆이나 위로 쌓는 그래프가 가능

    - histogram(분포 차트), boxplot 등의 종류가 있음

 

  🔥 seaborn: 통계적 데이터 시각화(Statistical data visualization)

    - matplotlib를 좀 더 쉽게하기 위해 사용

    - 복잡한 그래프를 간단하게 만들 수 있는 wrapper(간단 코드 + 예쁜 결과)

    - Basic: matplotlib와 같은 기복적인 plot으로 손쉬운 설정으로 데이터 산출

    - lineplot, scatterplot, countplot, regplot(hue - 카테고리 별 data 보는 것 가능), FacetGrid 등이 존재

    - conda install seaborn  ->  import seaborn as sns

 

📍 통계학 맛보기

    - 통계적 모델링은 적절한 가정 위에서 확률분포를 측정(inference)하는 것이 목표이며, 기계학습과 통계학이 공통적으로 추구하는 목표.

    - BUT, 유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확하게 알아낸다는 것은 불가능하므로, 근사적으로 확률분포를 추정한다.

 

    - 모수적방법론: data가 특정 확률 분포를 따른다고 신험적으로(a priori) 가정한 후 그 분포를 결정하는 모수(parameter)를 추정하는 방법

    - 비모수적방법론: 특정 확률분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연함

      -> 모수, 비모수의 차이는 '가정'의 차이이다.

 

    - 기계적으로 확률분포가정X, 데이터를 생성하는 원리를 먼저 고려해 볼 것! -> 모수를 추정 후 검증하는 과정이 중요

 

    - 정규분포의 모수는 평균과 분산으로 이를 추정하는 통계량(statistic)은 다음과 같다.

 

  🔥 표집분포(Sampling Distribution)

    - 통계량의 확률분포로 N이 커질수록 정규분포를 따름(중심극한정리에 따라)

 

  🔥 최대 가능도 추정법(MLE, Maximum Likelihood Estimation)

    - 이론적으로 가장 가능성이 높은 모수를 추정하는 방법

모수 theta를 따르는 분포가 x를 관찰할 가능성

    - 데이터 집합 X가 독립적으로 추출되었을 경우 로그 가능도를 최적화

 

 

  📌 왜 로그가능도를 사용하나요?   

- 로그 가능도를 최적화하는 모수 theta는 가능도를 최적화하는 MLE이다.   

- BUT, 데이터가 수억단위가 될 경우, 컴퓨터의 정확도로는 가능도 계산이 불가능하다. 그렇기 때문에 데이터가 독립일 경우, 로그를 사용해 컴퓨터로 연산이 가능하다.(연산량의 감소 O(n^2) => O(n))   

- 대게 손실함수의 경우 경사하강법 사용 -> 음의 로그가능도를 최적화하면 됨

 

  🔥 DL에서의 최대 가능도 추정법

    - 가중치 theta라 했을때, 분류 문제에서 Softmax vector는 카테고리 분포의 모수를 모데일링

    - one-hot vector로 표현한 정답 레이블 y를 관찰 데이터로 이용해 확률 분포인 softmax vector의 로그 가능도를 최적화 할 수 있다.

 

  🔥 확률분포의 거리

    - 기계학습에서 사용되는 손실 함수들은 모델이 학습하는 확률분포와 데이터에서 관찰되는 확률분포의 거리를 통해 유도

    - 데이터 공간에 두개의 확률 분포 P(x), Q(x)의 거리를 구하기 위한 기법

      -> 총변동거리(TV, Total Variation Distance)

      -> 쿨백-라이블러 발산(KL, Kullback-Leibler Divergence)

      -> 바슈타인 거리(Wasserstein Distance)

 

  📌 쿨백-라이블러 발산

    - 분류 문제에서 정답레이블(P), 모델 예측(Q)를 최소화하는 것으로 학습 가능

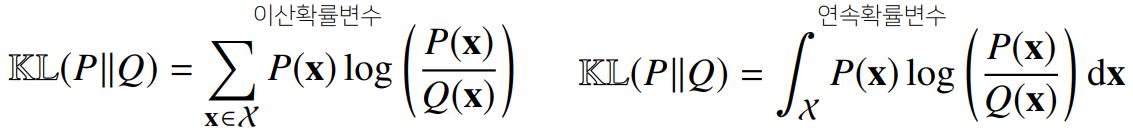
    - 위의 식을 아래와 같이 분해할 수 있다.